利用者:位相空間を中和/sandbox/1
利用者:位相空間を中和/sandbox/2
スペクトル系列 (スペクトルけいれつ、英 : Spectral sequence )とは、ホモロジー代数学 や代数的位相幾何学 で用いられる、ホモロジー群を逐次近似により計算する方法のことである。スペクトル系列は完全系列 の一般化であり、ジャン・ルレイ によって初めて用いられたとき[1] 代数的位相幾何学 、代数幾何学 、ホモロジー代数学 といった分野において重要な計算ツールとなっている。
ジャン・ルレイは代数的位相幾何学 の研究の過程で層 の概念を導入し、そして層係数コホモロジー を計算する問題に向き合うことになった。層係数コホモロジーを計算するために、ルレイは現在ルレイ・スペクトル系列 (英語版 ) 層の順像 (押し出しとも呼ばれる)のコホモロジー群とを、無限回の計算過程を通じて関係付けるものである。ルレイは、順像のコホモロジー群は自然に鎖複体 となることに気づき、したがってコホモロジーのコホモロジーを取れることに気付いた。これは元の層のコホモロジーにはなっていないが、ある意味ではそれに一歩近づいたものになっている。そして、コホモロジーのコホモロジーがまた鎖複体になるので、これのコホモロジーをまた取ることができ、この計算をずっと繰り返すことができる。この計算ステップを無限回繰り返した後の極限が、元の層のコホモロジー群と本質的に同じものとなっている。
ルレイの計算手法が幅広い状況に適用できることはすぐに明らかとなった。ファイブレーション (英語版 ) 導来関手 が関係する代数学的な状況で、複数の(コ)ホモロジー群を婉曲的にではあるが関係付けてくれるスペクトル系列が数多く発見された。導来圏 の導入によりその理論的な重要性は減ったが、今でもスペクトル系列はもっとも有効な計算ツールであり続けている。たとえスペクトル系列に計算不可能な項が多く含まれている状況であったとしても、スペクトル系列は有効に使うことのできる計算ツールである。
その反面、スペクトル系列は膨大な情報を持っているがゆえに会得や使用に困難が伴う。スペクトル系列が持っている情報は、3次元の格子状にアーベル群 もしくは環上の加群 を配置したものとなっていることが多い。最も取り扱いが簡単なスペクトル系列は、最終的には潰れる(collapse)、つまり列を進めてみてもそれ以上なんの情報も得られなくなるものである。このような場合でなくとも、種々のトリックを用いてスペクトル系列から有用な情報を引き出せることが多い。
A
{\displaystyle {\mathcal {A}}}
(
E
,
d
)
{\displaystyle (E,d)}
(
E
′
,
d
′
)
{\displaystyle (E',d')}
φ
:
E
→
E
′
{\displaystyle \varphi ~:~E\to E'}
d
′
∘
φ
=
φ
∘
d
{\displaystyle d'\circ \varphi =\varphi \circ d}
(
E
,
d
)
{\displaystyle (E,d)}
(
E
′
,
d
′
)
{\displaystyle (E',d')}
φ
:
(
E
,
d
)
→
(
E
′
,
d
′
)
{\displaystyle \varphi ~:~(E,d)\to (E',d')}
とみなすことで
A
{\displaystyle {\mathcal {A}}}
定理 ― アーベル圏
A
{\displaystyle {\mathcal {A}}}
A
{\displaystyle {\mathcal {A}}}
[3]
微分対象
(
E
,
d
)
{\displaystyle (E,d)}
H
(
E
,
d
)
:=
K
e
r
d
/
I
m
d
{\displaystyle H(E,d):=\mathrm {Ker} d/\mathrm {Im} d}
と定義する。
ここで
Z
>
0
{\displaystyle \mathbb {Z} _{>0}}
Z
>
0
=
{
1
,
2
,
3
,
…
}
{\displaystyle \mathbb {Z} _{>0}=\{1,2,3,\ldots \}}
アーベル圏
A
{\displaystyle {\mathcal {A}}}
E
=
(
E
r
,
d
r
)
r
∈
Z
>
0
{\displaystyle \mathbf {E} =(E^{r},d^{r})_{r\in \mathbb {Z} _{>0}}}
Z
r
{\displaystyle Z^{r}}
B
r
{\displaystyle B^{r}}
K
e
r
d
r
↠
Z
r
/
B
r
=
H
(
E
r
,
d
r
)
{\displaystyle \mathrm {Ker} d^{r}\twoheadrightarrow Z^{r}/B^{r}=H(E^{r},d^{r})}
I
m
d
r
↠
Z
r
/
B
r
=
H
(
E
r
,
d
r
)
{\displaystyle \mathrm {Im} d^{r}\twoheadrightarrow Z^{r}/B^{r}=H(E^{r},d^{r})}
Z
r
+
1
{\displaystyle Z^{r+1}}
B
r
+
1
{\displaystyle B^{r+1}}
A
{\displaystyle {\mathcal {A}}}
R -加群の圏の場合は準同型定理 を使って具体的に構成できる(対応定理 を参照)。
Z
r
{\displaystyle Z^{r}}
B
r
{\displaystyle B^{r}}
B
1
⊂
B
2
⊂
⋯
⊂
B
r
⊂
⋯
⊂
Z
r
⊂
⋯
⊂
Z
2
⊂
Z
1
{\displaystyle B^{1}\subset B^{2}\subset \cdots \subset B^{r}\subset \cdots \subset Z^{r}\subset \cdots \subset Z^{2}\subset Z^{1}}
が成立する[6]
これを踏まえてスペクトル系列
E
=
(
E
r
,
d
r
)
r
∈
Z
>
0
{\displaystyle \mathbf {E} =(E^{r},d^{r})_{r\in \mathbb {Z} _{>0}}}
上記の定義に2つ留意点を述べる。第一に、本項では文献[6]
Z
∞
=
∩
r
Z
r
{\displaystyle Z^{\infty }=\cap _{r}Z^{r}}
B
∞
=
∪
r
B
r
{\displaystyle B^{\infty }=\cup _{r}B^{r}}
R -加群の場合の表記であり、一般のアーベル圏の場合はそれぞれ圏論的な意味での極限と余極限 で定義する。
[8] 河田 p.272では各
E
r
{\displaystyle E^{r}}
E
r
=
{
E
p
,
q
r
}
p
,
q
{\displaystyle E^{r}=\{E_{p,q}^{r}\}_{p,q}}
p 、q に対しあるr0 が存在し、
E
p
,
q
r
0
≃
E
p
,
q
r
0
+
1
≃
E
p
,
q
r
0
+
2
⋯
{\displaystyle E_{p,q}^{r_{0}}\simeq E_{p,q}^{r_{0}+1}\simeq E_{p,q}^{r_{0}+2}\cdots }
本節ではスペクトル系列を構成する一般的手法である完全対 について述べる。既知のすべてのスペクトル系列は完全対から構成されている[9]
完全対の定義の背後にあるモチベーションを述べるために以下の具体例を考える。
C
∗
=
(
C
n
,
∂
n
)
n
∈
Z
{\displaystyle C_{*}=(C_{n},\partial _{n})_{n\in \mathbb {Z} }}
Z
{\displaystyle \mathbb {Z} }
チェイン複体 とし、p を素数 とし、短完全系列
0
⟶
C
∗
⟶
×
p
C
∗
⟶
π
C
∗
⊗
Z
Z
/
p
Z
⟶
0
{\displaystyle 0\longrightarrow C_{*}{\overset {\times p}{\longrightarrow }}C_{*}{\overset {\pi }{\longrightarrow }}C_{*}\otimes _{\mathbb {Z} }\mathbb {Z} /p\mathbb {Z} \longrightarrow 0}
を考える。ここで「
×
p
{\displaystyle \times p}
p 倍する写像であり、π は
c
↦
c
⊗
1
{\displaystyle c\mapsto c\otimes 1}
短完全系列が誘導する長完全系列
⋯
⟶
∂
∗
H
n
(
C
∗
;
Z
)
⟶
×
p
H
n
(
C
∗
;
Z
)
→
π
∗
H
n
(
C
∗
;
Z
/
p
Z
)
⟶
∂
∗
H
n
−
1
(
C
∗
;
Z
)
⟶
×
p
⋯
{\displaystyle \cdots {\overset {\partial _{*}}{\longrightarrow }}H_{n}(C_{*};\mathbb {Z} ){\overset {\times p}{\longrightarrow }}H_{n}(C_{*};\mathbb {Z} ){\overset {\pi _{*}}{\to }}H_{n}(C_{*};\mathbb {Z} /p\mathbb {Z} ){\overset {\partial _{*}}{\longrightarrow }}H_{n-1}(C_{*};\mathbb {Z} ){\overset {\times p}{\longrightarrow }}\cdots }
を作ることができる[10] [11]
(
A
,
∂
)
{\displaystyle (A,\partial )}
A
{\displaystyle {\mathcal {A}}}
[注 2]
α
:
A
→
A
{\displaystyle \alpha ~:~A\to A}
A
{\displaystyle {\mathcal {A}}}
余核 への射
π
:
A
→
C
o
i
m
(
α
)
{\displaystyle \pi ~:~A\to \mathrm {Coim} (\alpha )}
0
⟶
A
⟶
α
A
⟶
π
C
o
i
m
(
α
)
⟶
0
{\displaystyle 0\longrightarrow A{\overset {\alpha }{\longrightarrow }}A{\overset {\pi }{\longrightarrow }}\mathrm {Coim} (\alpha )\longrightarrow 0}
を考え、この完全系列が誘導する長完全系列
⋯
⟶
π
∗
H
(
C
o
i
m
(
α
)
)
⟶
∂
∗
H
(
A
)
⟶
α
∗
H
(
A
)
⟶
π
∗
H
(
C
o
i
m
(
α
)
)
⟶
∂
∗
⋯
{\displaystyle \cdots {\overset {\pi _{*}}{\longrightarrow }}H(\mathrm {Coim} (\alpha )){\overset {\partial _{*}}{\longrightarrow }}H(A){\overset {\alpha _{*}}{\longrightarrow }}H(A){\overset {\pi _{*}}{\longrightarrow }}H(\mathrm {Coim} (\alpha )){\overset {\partial _{*}}{\longrightarrow }}\cdots }
を考えることができる[12]
H
(
A
)
−
−
−
−
−
−
−
⟶
α
∗
H
(
A
)
∂
∗
↖
↙
π
∗
H
(
C
o
i
m
(
α
)
)
{\displaystyle {\begin{array}{rcl}H(A)&{\overset {\alpha _{*}}{-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!\longrightarrow }}&H(A)\\\partial _{*}\nwarrow &&\swarrow \pi _{*}\\&H(\mathrm {Coim} (\alpha ))&\end{array}}}
1 )
以上を踏まえて以下の定義をする:
完全対
(
D
,
E
,
α
,
β
,
γ
)
{\displaystyle (D,E,\alpha ,\beta ,\gamma )}
d
=
β
∘
γ
{\displaystyle d=\beta \circ \gamma }
とすると、
d
∘
d
=
0
{\displaystyle d\circ d=0}
となるので、
(
E
,
d
)
{\displaystyle (E,d)}
(
E
1
,
d
1
)
=
(
E
,
d
)
{\displaystyle (E_{1},d_{1})=(E,d)}
となるスペクトル系列
(
E
n
,
d
n
)
n
∈
Z
>
0
{\displaystyle (E_{n},d_{n})_{n\in \mathbb {Z} _{>0}}}
(
D
,
E
,
α
,
β
,
γ
)
{\displaystyle (D,E,\alpha ,\beta ,\gamma )}
導来完全対は以下のように定義される:
定義・定理 ―
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
A
{\displaystyle {\mathcal {A}}}
d
1
=
β
1
∘
γ
1
{\displaystyle d^{1}=\beta ^{1}\circ \gamma ^{1}}
D
2
:=
I
m
D
1
{\displaystyle D^{2}:=\mathrm {Im} D^{1}}
E
2
:=
H
(
E
1
,
d
1
)
{\displaystyle E^{2}:=H(E^{1},d^{1})}
とし、自然な全射
π
:
K
e
r
d
1
→
E
2
=
K
e
r
d
1
/
I
m
d
1
{\displaystyle \pi ~:~\mathrm {Ker} d^{1}\to E^{2}=\mathrm {Ker} d^{1}/\mathrm {Im} d^{1}}
を使って、
α
2
:
D
2
→
D
2
{\displaystyle \alpha ^{2}~:~D^{2}\to D^{2}}
D
2
↪
D
1
→
α
1
D
2
{\displaystyle D^{2}\hookrightarrow D^{1}{\overset {\alpha ^{1}}{\to }}D^{2}}
β
2
:
D
2
→
E
2
{\displaystyle \beta ^{2}~:~D^{2}\to E^{2}}
π
∘
β
1
=
β
2
∘
α
1
{\displaystyle \pi \circ \beta ^{1}=\beta ^{2}\circ \alpha ^{1}}
[注 3]
γ
2
:
E
2
→
D
2
{\displaystyle \gamma ^{2}~:~E^{2}\to D^{2}}
α
1
∘
γ
1
=
γ
2
∘
π
{\displaystyle \alpha ^{1}\circ \gamma ^{1}=\gamma ^{2}\circ \pi }
[注 3] とすると、α2 、β2 、γ2 はwell-defined であり、
D
2
−
−
⟶
α
2
D
2
γ
2
↖
↙
β
2
E
2
{\displaystyle {\begin{array}{ccc}D^{2}&{\overset {\alpha ^{2}}{-\!\!\!-\!\!\!\longrightarrow }}&D^{2}\\\gamma ^{2}\nwarrow &&\swarrow \beta ^{2}\\&E^{2}&\end{array}}}
は完全対となる[13]
(
D
2
,
E
2
,
α
2
,
β
2
,
γ
2
)
{\displaystyle (D^{2},E^{2},\alpha ^{2},\beta ^{2},\gamma ^{2})}
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
導来完全対 [14] 英 : deived couple [15] [16]
A
{\displaystyle {\mathcal {A}}}
R に対するR -加群の圏である場合にはβ2 、γ2 は以下のように具体的に書ける[17]
β
2
(
α
1
(
x
)
)
=
[
β
1
(
x
)
]
{\displaystyle \beta ^{2}(\alpha ^{1}(x))=[\beta ^{1}(x)]}
γ
2
(
[
z
]
)
=
γ
1
(
z
)
{\displaystyle \gamma ^{2}([z])=\gamma ^{1}(z)}
ここで
[
⋅
]
{\displaystyle [\cdot ]}
d1 によるホモロジー類を表す。
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
A
{\displaystyle {\mathcal {A}}}
再帰的 な定義が可能である:
(
D
r
,
E
r
,
α
r
,
β
r
,
γ
r
)
{\displaystyle (D^{r},E^{r},\alpha ^{r},\beta ^{r},\gamma ^{r})}
(
D
r
−
1
,
E
r
−
1
,
α
r
−
1
,
β
r
−
1
,
γ
r
−
1
)
{\displaystyle (D^{r-1},E^{r-1},\alpha ^{r-1},\beta ^{r-1},\gamma ^{r-1})}
定義 ― 上述のようにして定義した
(
D
r
,
E
r
,
α
r
,
β
r
,
γ
r
)
{\displaystyle (D^{r},E^{r},\alpha ^{r},\beta ^{r},\gamma ^{r})}
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
第r 導来完全対 (英 : r -th derived couple[18] [注 4]
このように第r 導来完全対を定義して、
d
r
:=
β
r
∘
γ
r
{\displaystyle d^{r}:=\beta ^{r}\circ \gamma ^{r}}
{
d
r
∘
d
r
=
0
E
r
+
1
=
H
(
E
r
,
d
r
)
{\displaystyle {\begin{cases}d^{r}\circ d^{r}=0\\E^{r+1}=H(E^{r},d^{r})\end{cases}}}
であったので、
E
=
(
E
r
,
d
r
)
r
∈
Z
≥
1
{\displaystyle \mathbf {E} =(E^{r},d^{r})_{r\in \mathbb {Z} _{\geq 1}}}
定義 ― 上述のようにして定義される
E
=
(
E
r
,
d
r
)
r
∈
Z
≥
1
{\displaystyle \mathbf {E} =(E^{r},d^{r})_{r\in \mathbb {Z} _{\geq 1}}}
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
により定まるスペクトル系列 (英 : spectral sequence determined by the exact couple [20]
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
により生み出されたスペクトル系列 (英 : spectral sequence yielded by the exact couple [21]
D
r
{\displaystyle D^{r}}
d
r
=
β
r
∘
γ
r
{\displaystyle d^{r}=\beta ^{r}\circ \gamma ^{r}}
E
r
{\displaystyle E^{r}}
βr の定義域である
D
r
{\displaystyle D^{r}}
1 n 導来完全対を作ってそこから上記のようにして作ったスペクトル系列をボックシュタイン・スペクトル系列 (英語版 )
本説では上述した完全対からスペクトル系列を作る操作は関手 とみなす事ができる事を見る。このために、まず完全対の圏とスペクトル系列の圏を定義する。
アーベル圏
A
{\displaystyle {\mathcal {A}}}
E
C
=
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle \mathbf {EC} =(D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
E
C
′
=
(
D
′
1
,
E
′
1
,
α
′
1
,
β
′
1
,
γ
′
1
)
{\displaystyle \mathbf {EC} '=(D'^{1},E'^{1},\alpha '^{1},\beta '^{1},\gamma '^{1})}
κ
:
D
1
→
D
′
1
{\displaystyle \kappa ~:~D^{1}\to D'^{1}}
κ
¯
:
E
1
→
E
′
1
{\displaystyle {\bar {\kappa }}~:~E^{1}\to E'^{1}}
の組
(
κ
,
κ
¯
)
{\displaystyle (\kappa ,{\bar {\kappa }})}
α
′
∘
κ
=
κ
∘
α
{\displaystyle \alpha '\circ \kappa =\kappa \circ \alpha }
β
′
∘
κ
=
κ
¯
∘
β
{\displaystyle \beta '\circ \kappa ={\bar {\kappa }}\circ \beta }
γ
′
∘
κ
¯
=
κ
∘
γ
{\displaystyle \gamma '\circ {\bar {\kappa }}=\kappa \circ \gamma }
E
C
{\displaystyle \mathbf {EC} }
E
C
′
{\displaystyle \mathbf {EC} '}
A
{\displaystyle {\mathcal {A}}}
E
C
A
{\displaystyle {\mathcal {EC}}_{\mathcal {A}}}
[22]
アーベル圏
A
{\displaystyle {\mathcal {A}}}
E
=
(
E
n
,
d
n
)
n
∈
Z
>
0
{\displaystyle \mathbf {E} =(E_{n},d_{n})_{n\in \mathbb {Z} _{>0}}}
E
′
=
(
E
n
′
,
d
n
′
)
n
∈
Z
>
0
{\displaystyle \mathbf {E} '=(E'_{n},d'_{n})_{n\in \mathbb {Z} _{>0}}}
(
φ
n
)
n
∈
Z
>
0
{\displaystyle (\varphi _{n})_{n\in \mathbb {Z} _{>0}}}
φ
n
:
E
1
→
E
1
′
{\displaystyle \varphi _{n}~:~E_{1}\to E'_{1}}
φ
n
+
1
=
H
(
φ
n
)
{\displaystyle \varphi _{n+1}=H(\varphi _{n})}
を
E
{\displaystyle \mathbf {E} }
E
′
{\displaystyle \mathbf {E} '}
A
{\displaystyle {\mathcal {A}}}
S
A
{\displaystyle {\mathcal {S}}_{\mathcal {A}}}
[22]
H
{\displaystyle H}
A
{\displaystyle {\mathcal {A}}}
E
C
A
{\displaystyle {\mathcal {EC}}_{\mathcal {A}}}
A
{\displaystyle {\mathcal {A}}}
S
A
{\displaystyle {\mathcal {S}}_{\mathcal {A}}}
完全対
E
C
{\displaystyle \mathbf {EC} }
S
(
E
C
)
{\displaystyle S(\mathbf {EC} )}
射
(
κ
,
κ
¯
)
:
E
C
→
E
C
′
{\displaystyle (\kappa ,{\bar {\kappa }})~:~\mathbf {EC} \to \mathbf {EC} '}
S
(
κ
,
κ
¯
)
=
(
φ
n
)
n
∈
Z
>
0
:
S
(
E
C
)
→
S
(
E
C
′
)
{\displaystyle S(\kappa ,{\bar {\kappa }})=(\varphi _{n})_{n\in \mathbb {Z} _{>0}}~:~S(\mathbf {EC} )\to S(\mathbf {EC} ')}
φ
1
=
κ
¯
{\displaystyle \varphi _{1}={\bar {\kappa }}}
φ
n
+
1
=
H
(
φ
n
)
{\displaystyle \varphi _{n+1}=H(\varphi _{n})}
ここで
(
D
n
,
E
n
,
α
n
,
β
n
,
γ
n
)
{\displaystyle (D_{n},E_{n},\alpha _{n},\beta _{n},\gamma _{n})}
E
C
{\displaystyle \mathbf {EC} }
n 導来完全対である。
定義 ― 上述のように定義した関手
S
:
E
C
A
→
S
A
{\displaystyle S~:~{\mathcal {EC}}_{\mathcal {A}}\to {\mathcal {S}}_{\mathcal {A}}}
スペクトル系列関手 (英 : spectral sequence functor )という[23]
本章では、フィルター付き微分対象 を定義し、フィルター付き微分対象から完全対が得られ、したがってそこからさらにスペクトル系列を得られる事を見る。
(
A
,
F
)
{\displaystyle (A,F)}
(
A
′
,
F
′
)
{\displaystyle (A',F')}
A
{\displaystyle {\mathcal {A}}}
φ
:
A
→
A
′
{\displaystyle \varphi ~:~A\to A'}
φ
(
F
p
A
)
⊂
F
p
′
A
′
{\displaystyle \varphi (F_{p}A)\subset F'_{p}A'}
p
∈
Z
{\displaystyle p\in \mathbb {Z} }
となるものを
(
A
,
F
)
{\displaystyle (A,F)}
(
A
′
,
F
′
)
{\displaystyle (A',F')}
A
{\displaystyle {\mathcal {A}}}
フィルター付き対象の圏
F
i
l
(
A
)
{\displaystyle \mathrm {Fil} ({\mathcal {A}})}
[25]
定義 ―
A
{\displaystyle {\mathcal {A}}}
フィルター付き微分対象 (英 : filtered differential object [26]
定義から明らかなようにフィルター付き微分対象とは、組
(
A
,
F
,
∂
)
{\displaystyle (A,F,\partial )}
(
A
,
∂
)
{\displaystyle (A,\partial )}
A
{\displaystyle {\mathcal {A}}}
(
A
,
F
)
{\displaystyle (A,F)}
A
{\displaystyle {\mathcal {A}}}
p に対し
∂
F
p
A
⊃
F
p
A
{\displaystyle \partial F_{p}A\supset F_{p}A}
となるものを指す[27]
∂ のFp A への制限
∂
|
F
p
A
{\displaystyle \partial |_{F_{p}A}}
(
F
p
A
,
∂
|
F
p
A
)
{\displaystyle (F_{p}A,\partial |_{F_{p}A})}
そこで微分対象の短完全系列
0
⟶
F
p
−
1
A
⟶
F
p
A
⟶
F
p
A
/
F
p
−
1
A
⟶
0
{\displaystyle 0\longrightarrow F_{p-1}A\longrightarrow F_{p}A\longrightarrow F_{p}A/F_{p-1}A\longrightarrow 0}
を考えると、前述のようにそこから長完全系列
H
(
F
p
−
1
A
)
−
−
−
−
−
−
−
⟶
H
(
F
p
A
)
↖
↙
H
(
F
p
A
/
F
p
−
1
A
)
{\displaystyle {\begin{array}{rcl}H(F_{p-1}A)&-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!\longrightarrow &H(F_{p}A)\\\nwarrow &&\swarrow \\&H(F_{p}A/F_{p-1}A)&\end{array}}}
を構成できる。そこで
D
=
(
H
(
F
p
A
)
)
p
∈
Z
{\displaystyle D=(H(F_{p}A))_{p\in \mathbb {Z} }}
E
=
(
H
(
F
p
A
/
F
p
−
1
A
)
)
p
∈
Z
{\displaystyle E=(H(F_{p}A/F_{p-1}A))_{p\in \mathbb {Z} }}
とすると、完全対
D
−
−
−
−
⟶
D
↖
↙
E
{\displaystyle {\begin{array}{rcl}D~~~&-\!\!\!-\!\!\!-\!\!\!-\!\!\!\longrightarrow &~~~D\\~~~~~~~~\nwarrow &&\swarrow ~~~~~~~~\\&E&\end{array}}}
が構成でき、この完全対からスペクトル系列を構成できる。
以上の完全対の定義を踏まえ、以下の定義を導入する。
G
r
(
A
)
{\displaystyle \mathrm {Gr} ({\mathcal {A}})}
A
{\displaystyle {\mathcal {A}}}
(
A
p
)
p
∈
Z
{\displaystyle (A_{p})_{p\in \mathbb {Z} }}
A
{\displaystyle {\mathcal {A}}}
(
f
p
)
p
∈
Z
{\displaystyle (f_{p})_{p\in \mathbb {Z} }}
f
p
:
A
p
→
A
p
′
{\displaystyle f_{p}~:~A_{p}\to A'_{p}}
gr は
g
r
:
F
i
l
(
A
)
→
G
r
(
A
)
{\displaystyle \mathrm {gr} ~:~\mathrm {Fil} ({\mathcal {A}})\to \mathrm {Gr} ({\mathcal {A}})}
という関手とみなせる。ここで射
φ
:
(
A
,
F
)
→
(
A
′
,
F
′
)
{\displaystyle \varphi ~:~(A,F)\to (A',F')}
g
r
(
φ
)
=
(
φ
p
)
p
∈
Z
{\displaystyle \mathrm {gr} (\varphi )=(\varphi _{p})_{p\in \mathbb {Z} }}
φ
|
F
p
A
{\displaystyle \varphi |_{F_{p}A}}
φ
p
:
F
p
A
/
F
p
−
1
A
→
F
p
′
A
′
/
F
p
−
1
′
A
′
{\displaystyle \varphi _{p}~:~F_{p}A/F_{p-1}A\to F'_{p}A'/F'_{p-1}A'}
すなわち、
A
{\displaystyle {\mathcal {A}}}
(
C
q
,
{
F
p
C
q
}
p
∈
Z
,
∂
q
)
q
∈
Z
{\displaystyle (C_{q},\{F_{p}C_{q}\}_{p\in \mathbb {Z} },\partial _{q})_{q\in \mathbb {Z} }}
A
{\displaystyle {\mathcal {A}}}
(
C
q
,
{
F
p
C
q
}
p
∈
Z
)
{\displaystyle (C_{q},\{F_{p}C_{q}\}_{p\in \mathbb {Z} })}
∂
q
:
C
q
→
C
q
−
1
{\displaystyle \partial _{q}~:~C_{q}\to C_{q-1}}
∂
(
F
p
C
q
)
⊂
F
p
C
q
−
1
{\displaystyle \partial (F_{p}C_{q})\subset F_{p}C_{q-1}}
p
,
q
∈
Z
{\displaystyle p,q\in \mathbb {Z} }
を満たすものを指す。フィルター付きチェイン複体は自然にフィルター付き微分対象とみなせるので、前述のように完全対を構成できる。
D
:=
(
D
p
,
q
)
p
,
q
∈
Z
where
D
p
,
q
:=
H
p
+
q
(
F
p
C
)
E
:=
(
E
p
,
q
)
p
,
q
∈
Z
where
E
p
,
q
:=
H
p
+
q
(
F
p
C
/
F
p
−
1
C
)
{\displaystyle {\begin{aligned}D&:=(D_{p,q})_{p,q\in \mathbb {Z} }{\text{ where }}D_{p,q}:=H_{p+q}(F_{p}C)\\E&:=(E_{p,q})_{p,q\in \mathbb {Z} }{\text{ where }}E_{p,q}:=H_{p+q}(F_{p}C/F_{p-1}C)\end{aligned}}}
として[注 5]
D
−
−
−
−
⟶
(
1
,
−
1
)
D
(
−
1
,
0
)
↖
↙
(
0
,
0
)
E
{\displaystyle {\begin{array}{rcl}D~~~&{\overset {(1,-1)}{-\!\!\!-\!\!\!-\!\!\!-\!\!\!\longrightarrow }}&~~~D\\~~~~~~~~{}_{(-1,0)}\nwarrow &&\swarrow {}_{(0,0)}~~~~~~~~\\&E&\end{array}}}
が構成できる[33]
D
⟶
(
1
,
−
1
)
D
{\displaystyle D{\overset {(1,-1)}{\longrightarrow }}D}
p が1増え、q が1減る事を意味する。
定理 ― 記号を上述のように取るとき、上述の完全対から定まる第r 導来完全対
(
D
r
,
E
r
,
α
r
,
β
r
,
γ
r
)
{\displaystyle (D^{r},E^{r},\alpha ^{r},\beta ^{r},\gamma ^{r})}
D
r
−
−
−
−
⟶
(
1
,
−
1
)
α
r
D
r
(
−
1
,
0
)
↖
↙
(
1
−
r
,
r
−
1
)
E
r
{\displaystyle {\begin{array}{rcl}D^{r}~~~&{\underset {\alpha ^{r}}{\overset {(1,-1)}{-\!\!\!-\!\!\!-\!\!\!-\!\!\!\longrightarrow }}}&~~~D^{r}\\~~~~~~~~{}_{(-1,0)}\nwarrow &&\swarrow {}_{(1-r,r-1)}~~~~~~~~\\&E^{r}&\end{array}}}
である[34]
d
r
:=
β
r
∘
γ
r
{\displaystyle d^{r}:=\beta ^{r}\circ \gamma ^{r}}
E
r
−
−
−
⟶
d
r
(
−
r
,
r
−
1
)
E
r
{\displaystyle E_{r}{\underset {(-r,r-1)}{\overset {d^{r}}{-\!\!\!-\!\!\!-\!\!\!\longrightarrow }}}E_{r}}
である[34]
環 上の加群 のようなアーベル圏 を一つ固定する。コホモロジー的 なスペクトル系列 とは、一つの非負整数
r
0
{\displaystyle r_{0}}
r
≥
r
0
{\displaystyle r\geq r_{0}}
シート (紙 1枚のイメージ)、ページ 、もしくは項 と呼ばれる対象
E
r
{\displaystyle E_{r}}
境界写像 、もしくは微分 と呼ばれる、自己準同型
d
r
:
E
r
→
E
r
{\displaystyle d_{r}\colon E_{r}\to E_{r}}
d
r
∘
d
r
=
0
{\displaystyle d_{r}\circ d_{r}=0}
E
r
+
1
{\displaystyle E_{r+1}}
E
r
{\displaystyle E_{r}}
d
r
{\displaystyle d_{r}}
H
(
E
r
)
{\displaystyle H(E_{r})}
通常、
E
r
+
1
{\displaystyle E_{r+1}}
H
(
E
r
)
{\displaystyle H(E_{r})}
E
r
+
1
{\displaystyle E_{r+1}}
E
r
{\displaystyle E_{r}}
導来(derived)対象 と呼ぶこともある[要出典 。
最も簡単な例は鎖複体 C• である。鎖複体のなすアーベル圏の対象である C• は微分 d を備えている。r 0 = 0 と置き、E 0 を C• とする。スペクトル系列を構成するためには E 1 は複体 H (C• ) としなけらればならず、i 番目の位置にあるものは C• の i 番目のホモロジー群となる。この新しい複体における唯一の自然な微分は零写像のみなので、d 1 = 0 と置く。
E
2
{\displaystyle E_{2}}
E
1
{\displaystyle E_{1}}
E 0 = C• Er = H (C• ) (全ての r ≥ 1)であるスペクトル系列を得られた。非自明な微分は0番目のシートにしか無いので、このスペクトル系列の項は1番目のシートで安定する。そのため、あとのステップには何の有益な情報も含まれていない。通常は、後のシートから有益な情報を得るためには、
E
r
{\displaystyle E_{r}}
今の次数のない簡単な例では r 0 に重要性は無かったが、実際には、ほとんどのスペクトル系列は環 R 上の2重次数つきの加群 (や環の層上の2重次数つきの加群の層 )の圏から生じる。このような場合は、シート1枚は2重次数つき加群であり、したがって2重次数1つにつき項が1つあり、シートはその直和に分解する。シートの各項の境界写像の直和として、シートの境界写像が定義される。その次数は r に応じて慣習的に固定されている。ホモロジー的なスペクトル系列 の場合は、項は
E
p
,
q
r
{\displaystyle E_{p,q}^{r}}
2重次数 (bidegree)は (− r ,r − 1) である。コホモロジー的なスペクトル系列の場合は、項は
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
2重次数 は (r , 1 − r ) である。(この2重次数の選び方は現実に自然に生じるものに即したものになっている。後段の2重複体についての例を参照のこと。)スペクトル系列によって、最初のシートの境界写像は r = 0、 r = 1、もしくは r = 2 に対応する次数を持つ。例えば、後で説明するフィルターつき複体のスペクトル系列では r 0 = 0、グロタンディーク・スペクトル系列 (英語版 ) r 0 = 2 である。r 0 は 0, 1, 2のいずれかであることが多い。
スペクトル系列の射 E → E' とは、定義により、写像 fr : Er → E'r の集まりであって、微分及び E 及び E' の r 番目と (r+1) 番目のシートのコホモロジーの間に与えられた同型写像と整合的であるものである。
[ 編集 ] E r r = 1 から始まるものとする。このとき、部分対象の列
0
=
B
0
⊂
B
1
⊂
B
2
⊂
⋯
⊂
B
r
⊂
⋯
⊂
Z
r
⊂
⋯
⊂
Z
2
⊂
Z
1
⊂
Z
0
=
E
1
{\displaystyle 0=B_{0}\subset B_{1}\subset B_{2}\subset \dots \subset B_{r}\subset \dots \subset Z_{r}\subset \dots \subset Z_{2}\subset Z_{1}\subset Z_{0}=E_{1}}
が存在し、
E
r
≃
Z
r
−
1
/
B
r
−
1
{\displaystyle E_{r}\simeq Z_{r-1}/B_{r-1}}
Z
0
=
E
1
,
B
0
=
0
{\displaystyle Z_{0}=E_{1},B_{0}=0}
Z
r
,
B
r
{\displaystyle Z_{r},B_{r}}
E
r
→
d
r
E
r
{\displaystyle E_{r}{\overset {d_{r}}{\to }}E_{r}}
Z
r
/
B
r
−
1
,
B
r
/
B
r
−
1
{\displaystyle Z_{r}/B_{r-1},B_{r}/B_{r-1}}
次に
Z
∞
=
∩
r
Z
r
,
B
∞
=
∪
r
B
r
{\displaystyle Z_{\infty }=\cap _{r}Z_{r},B_{\infty }=\cup _{r}B_{r}}
E
∞
=
Z
∞
/
B
∞
{\displaystyle E_{\infty }=Z_{\infty }/B_{\infty }}
と置く。これは極限項と呼ばれている。(もちろん、圏によってはそのような
E
∞
{\displaystyle E_{\infty }}
コホモロジー的なスペクトル系列の E2 シート 2重次数つきのスペクトル系列は膨大な量の把握すべきデータを持つが、これを視覚的に捉えるために広く使われている表示方法がある。r 、p 、q を2重次数つきスペクトル系列の3つの添字とする。r ごとに、方眼紙が1枚あると想像しよう。このシートの上で、p は水平方向、q は垂直方向の位置を表しているとしよう。そして、各マス目に対象
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
n = p + q と置いて、これをスペクトル系列のもう一つの別の自然な添字とすることもよく行われる。n は各シートにおいて北西から南東に対角的に走る。ホモロジー的な場合には、微分は2重次数 (−r , r − 1) を持つので、n は1減る。コホモロジー的な場合には n は1増える。r が0の場合は、微分は下もしくは上に1マス先にいる対象へ向かい、鎖複体の微分と同様になっている。r が1の場合は、微分は左もしくは右に1マス先にいる対象に向かう。r が2の場合は、微分はチェス のナイト が移動する位置にいる対象へ向かう。より大きな r の場合は、微分は一般化されたナイトが移動する位置にいる対象へ向かう。
スペクトル系列を初めて学習するときには、簡単な具体例で実際に計算を行ってみることが理解の助けになる。収束についてのより理論的で厳密な議論は後の節で行うが、この節については、スペクトル系列が増加フィルトレーション F を持つ H に収束するとは、
E
p
,
q
∞
=
F
p
H
p
+
q
/
F
p
−
1
H
p
+
q
{\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}/F_{p-1}H_{p+q}}
E
2
{\displaystyle E^{2}}
ギシン列 (英語版 )
E
p
,
q
r
{\displaystyle E_{p,q}^{r}}
p に対しては
E
p
,
q
2
=
0
{\displaystyle E_{p,q}^{2}=0}
E
2
{\displaystyle E^{2}}
⋮
⋮
⋮
⋮
⋯
0
E
0
,
2
2
E
1
,
2
2
0
⋯
⋯
0
E
0
,
1
2
E
1
,
1
2
0
⋯
⋯
0
E
0
,
0
2
E
1
,
0
2
0
⋯
⋯
0
E
0
,
−
1
2
E
1
,
−
1
2
0
⋯
⋮
⋮
⋮
⋮
{\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&E_{1,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&E_{1,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&E_{1,0}^{2}&0&\cdots \\\cdots &0&E_{0,-1}^{2}&E_{1,-1}^{2}&0&\cdots \\&\vdots &\vdots &\vdots &\vdots &\end{matrix}}}
となっている。この2番目のページの微分の次数は (-2, 1) なので、微分は
d
p
,
q
2
:
E
p
,
q
2
→
E
p
−
2
,
q
+
1
2
{\displaystyle d_{p,q}^{2}:E_{p,q}^{2}\to E_{p-2,q+1}^{2}}
という形をしていて、
d
0
,
q
2
:
E
0
,
q
2
→
0
{\displaystyle d_{0,q}^{2}:E_{0,q}^{2}\to 0}
d
1
,
q
2
:
E
1
,
q
2
→
0
{\displaystyle d_{1,q}^{2}:E_{1,q}^{2}\to 0}
なので、微分は全て零写像となっている。したがって、
E
∞
=
E
2
{\displaystyle E^{\infty }=E^{2}}
H
∗
{\displaystyle H_{*}}
0
=
F
−
1
H
n
⊂
F
0
H
n
⊂
⋯
⊂
F
n
H
n
=
H
n
{\displaystyle 0=F_{-1}H_{n}\subset F_{0}H_{n}\subset \dots \subset F_{n}H_{n}=H_{n}}
で与えられていて、
E
p
,
q
∞
=
F
p
H
p
+
q
/
F
p
−
1
H
p
+
q
{\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}/F_{p-1}H_{p+q}}
F
0
H
n
=
E
0
,
n
2
{\displaystyle F_{0}H_{n}=E_{0,n}^{2}}
F
1
H
n
/
F
0
H
n
=
E
1
,
n
−
1
2
{\displaystyle F_{1}H_{n}/F_{0}H_{n}=E_{1,n-1}^{2}}
F
2
H
n
/
F
1
H
n
=
0
{\displaystyle F_{2}H_{n}/F_{1}H_{n}=0}
F
3
H
n
/
F
2
H
n
=
0
{\displaystyle F_{3}H_{n}/F_{2}H_{n}=0}
0
→
E
0
,
n
2
→
H
n
→
E
1
,
n
−
1
2
→
0
{\displaystyle 0\to E_{0,n}^{2}\to H_{n}\to E_{1,n-1}^{2}\to 0}
が得られる[35]
E
p
,
q
r
{\displaystyle E_{p,q}^{r}}
q = 0, 1 の2行以外ゼロであるものを考える。このスペクトル系列は2番目のページで退化するとは限らないが、3番目のページでは微分の次数が (-3, 2) なのでそのページで退化する。分母がゼロであることに注意すると、
E
p
,
0
3
=
ker
(
d
:
E
p
,
0
2
→
E
p
−
2
,
1
2
)
{\displaystyle E_{p,0}^{3}=\operatorname {ker} (d:E_{p,0}^{2}\to E_{p-2,1}^{2})}
E
p
,
1
3
=
coker
(
d
:
E
p
+
2
,
0
2
→
E
p
,
1
2
)
{\displaystyle E_{p,1}^{3}=\operatorname {coker} (d:E_{p+2,0}^{2}\to E_{p,1}^{2})}
0
→
E
p
,
0
∞
→
E
p
,
0
2
→
d
E
p
−
2
,
1
2
→
E
p
−
2
,
1
∞
→
0
{\displaystyle 0\to E_{p,0}^{\infty }\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to E_{p-2,1}^{\infty }\to 0}
が成り立つ。先程の例と同様に、スペクトル系列がフィルトレーション F を持つ H に収束したとする。
F
p
−
2
H
p
/
F
p
−
3
H
p
=
E
p
−
2
,
2
∞
=
0
{\displaystyle F_{p-2}H_{p}/F_{p-3}H_{p}=E_{p-2,2}^{\infty }=0}
F
p
−
3
H
p
/
F
p
−
4
H
p
=
0
{\displaystyle F_{p-3}H_{p}/F_{p-4}H_{p}=0}
0
→
E
p
−
1
,
1
∞
→
H
p
→
E
p
,
0
∞
→
0
{\displaystyle 0\to E_{p-1,1}^{\infty }\to H_{p}\to E_{p,0}^{\infty }\to 0}
⋯
→
H
p
+
1
→
E
p
+
1
,
0
2
→
d
E
p
−
1
,
1
2
→
H
p
→
E
p
,
0
2
→
d
E
p
−
2
,
1
2
→
H
p
−
1
→
…
{\displaystyle \cdots \to H_{p+1}\to E_{p+1,0}^{2}{\overset {d}{\to }}E_{p-1,1}^{2}\to H_{p}\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to H_{p-1}\to \dots }
が得られる[36]
前節での計算は簡単に一般化できる。n を2以上の整数とし、球面上のファイブレーション (英語版 )
F
→
i
E
→
p
S
n
{\displaystyle F{\overset {i}{\to }}E{\overset {p}{\to }}S^{n}}
を考える。このとき、セール・スペクトル系列 (英語版 )
E
p
,
q
2
=
H
p
(
S
n
;
H
q
(
F
)
)
⇒
H
p
+
q
(
E
)
{\displaystyle E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))\Rightarrow H_{p+q}(E)}
がある。つまり、あるフィルトレーション
F
∙
{\displaystyle F_{\bullet }}
E
p
,
q
∞
=
F
p
H
p
+
q
(
E
)
/
F
p
−
1
H
p
+
q
(
E
)
{\displaystyle E_{p,q}^{\infty }=F_{p}H_{p+q}(E)/F_{p-1}H_{p+q}(E)}
H
p
(
S
n
)
{\displaystyle H_{p}(S^{n})}
p が0もしくは n の場合だけで、その場合は Z に等しいから、
E
p
,
q
2
{\displaystyle E_{p,q}^{2}}
p
=
0
,
n
{\displaystyle p=0,n}
E
2
{\displaystyle E^{2}}
⋮
⋮
⋮
⋮
⋮
⋮
⋯
0
E
0
,
2
2
0
⋯
0
E
n
,
2
2
0
⋯
⋯
0
E
0
,
1
2
0
⋯
0
E
n
,
1
2
0
⋯
⋯
0
E
0
,
0
2
0
⋯
0
E
n
,
0
2
0
⋯
{\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&0&\cdots &0&E_{n,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&0&\cdots &0&E_{n,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&0&\cdots &0&E_{n,0}^{2}&0&\cdots \\\end{matrix}}}
という形をしている。さらに、
p
=
0
,
n
{\displaystyle p=0,n}
普遍係数定理 により
E
p
,
q
2
=
H
p
(
S
n
;
H
q
(
F
)
)
=
H
q
(
F
)
{\displaystyle E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))=H_{q}(F)}
であるから、
E
2
{\displaystyle E^{2}}
⋮
⋮
⋮
⋮
⋮
⋮
⋯
0
H
2
(
F
)
0
⋯
0
H
2
(
F
)
0
⋯
⋯
0
H
1
(
F
)
0
⋯
0
H
1
(
F
)
0
⋯
⋯
0
H
0
(
F
)
0
⋯
0
H
0
(
F
)
0
⋯
{\displaystyle {\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&H_{2}(F)&0&\cdots &0&H_{2}(F)&0&\cdots \\\cdots &0&H_{1}(F)&0&\cdots &0&H_{1}(F)&0&\cdots \\\cdots &0&H_{0}(F)&0&\cdots &0&H_{0}(F)&0&\cdots \\\end{matrix}}}
と書ける。ゼロではない微分は
E
n
{\displaystyle E^{n}}
d
n
,
q
n
:
E
n
,
q
n
→
E
0
,
q
+
n
−
1
n
{\displaystyle d_{n,q}^{n}:E_{n,q}^{n}\to E_{0,q+n-1}^{n}}
だけであり、これは
d
n
,
q
n
:
H
q
(
F
)
→
H
q
+
n
−
1
(
F
)
{\displaystyle d_{n,q}^{n}:H_{q}(F)\to H_{q+n-1}(F)}
であるから、このスペクトル系列は
E
n
+
1
=
E
∞
{\displaystyle E^{n+1}=E^{\infty }}
E
n
+
1
{\displaystyle E^{n+1}}
0
→
E
n
,
q
−
n
∞
→
E
n
,
q
−
n
n
→
d
E
0
,
q
−
1
n
→
E
0
,
q
−
1
∞
→
0.
{\displaystyle 0\to E_{n,q-n}^{\infty }\to E_{n,q-n}^{n}{\overset {d}{\to }}E_{0,q-1}^{n}\to E_{0,q-1}^{\infty }\to 0.}
を得る。これをホモロジー群で書き直すと
0
→
E
n
,
q
−
n
∞
→
H
q
−
n
(
F
)
→
d
H
q
−
1
(
F
)
→
E
0
,
q
−
1
∞
→
0
{\displaystyle 0\to E_{n,q-n}^{\infty }\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F)\to E_{0,q-1}^{\infty }\to 0}
となる。これに出てくる2つの
E
∞
{\displaystyle E^{\infty }}
H
=
H
(
E
)
{\displaystyle H=H(E)}
F
1
H
q
/
F
0
H
q
=
E
1
,
q
−
1
∞
=
0
{\displaystyle F_{1}H_{q}/F_{0}H_{q}=E_{1,q-1}^{\infty }=0}
E
n
,
q
−
n
∞
=
F
n
H
q
/
F
0
H
q
{\displaystyle E_{n,q-n}^{\infty }=F_{n}H_{q}/F_{0}H_{q}}
F
n
H
q
=
H
q
{\displaystyle F_{n}H_{q}=H_{q}}
0
→
E
0
,
q
∞
→
H
q
→
E
n
,
q
−
n
∞
→
0
{\displaystyle 0\to E_{0,q}^{\infty }\to H_{q}\to E_{n,q-n}^{\infty }\to 0}
となる。これは完全系列
0
→
H
q
(
F
)
→
H
q
(
E
)
→
H
q
−
n
(
F
)
→
0
{\displaystyle 0\to H_{q}(F)\to H_{q}(E)\to H_{q-n}(F)\to 0}
である。以上の計算を全てまとめると、
⋯
→
H
q
(
F
)
→
i
∗
H
q
(
E
)
→
H
q
−
n
(
F
)
→
d
H
q
−
1
(
F
)
→
i
∗
H
q
−
1
(
E
)
→
H
q
−
n
−
1
(
F
)
→
…
{\displaystyle \dots \to H_{q}(F){\overset {i_{*}}{\to }}H_{q}(E)\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F){\overset {i_{*}}{\to }}H_{q-1}(E)\to H_{q-n-1}(F)\to \dots }
がわかった[37] ギシン列 (英語版 )
今の例で行ったような計算は、コホモロジー的なスペクトル系列に対しても簡単に適用できる。
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
0
=
F
n
+
1
H
n
⊂
F
n
H
n
⊂
⋯
⊂
F
0
H
n
=
H
n
{\displaystyle 0=F^{n+1}H^{n}\subset F^{n}H^{n}\subset \dots \subset F^{0}H^{n}=H^{n}}
を持つ H に収束、つまり
E
∞
p
,
q
=
F
p
H
p
+
q
/
F
p
+
1
H
p
+
q
{\displaystyle E_{\infty }^{p,q}=F^{p}H^{p+q}/F^{p+1}H^{p+q}}
p か q が負であれば
E
2
p
,
q
{\displaystyle E_{2}^{p,q}}
0
→
E
∞
0
,
1
→
E
2
0
,
1
→
d
E
2
2
,
0
→
E
∞
2
,
0
→
0.
{\displaystyle 0\to E_{\infty }^{0,1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to E_{\infty }^{2,0}\to 0.}
が成り立つ。同じ理由で
E
∞
1
,
0
=
E
2
1
,
0
{\displaystyle E_{\infty }^{1,0}=E_{2}^{1,0}}
F
2
H
1
=
0
{\displaystyle F^{2}H^{1}=0}
0
→
E
2
1
,
0
→
H
1
→
E
∞
0
,
1
→
0
{\displaystyle 0\to E_{2}^{1,0}\to H^{1}\to E_{\infty }^{0,1}\to 0}
となる。
F
3
H
2
=
0
{\displaystyle F^{3}H^{2}=0}
E
∞
2
,
0
⊂
H
2
{\displaystyle E_{\infty }^{2,0}\subset H^{2}}
5項完全系列 (英語版 )
0
→
E
2
1
,
0
→
H
1
→
E
2
0
,
1
→
d
E
2
2
,
0
→
H
2
{\displaystyle 0\to E_{2}^{1,0}\to H^{1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to H^{2}}
を得る。
E
p
,
q
r
{\displaystyle E_{p,q}^{r}}
q < 0 に対して
E
p
,
q
r
=
0
{\displaystyle E_{p,q}^{r}=0}
r ≥ 2 に対して
E
p
,
0
r
+
1
=
ker
(
d
:
E
p
,
0
r
→
E
p
−
r
,
r
−
1
r
)
{\displaystyle E_{p,0}^{r+1}=\operatorname {ker} (d:E_{p,0}^{r}\to E_{p-r,r-1}^{r})}
でなければならない(分母がゼロとなるので)。したがって、単射準同型の列
E
p
,
0
r
→
E
p
,
0
r
−
1
→
⋯
→
E
p
,
0
3
→
E
p
,
0
2
{\displaystyle E_{p,0}^{r}\to E_{p,0}^{r-1}\to \dots \to E_{p,0}^{3}\to E_{p,0}^{2}}
が存在する。これはエッジ写像(edge map)と呼ばれている。同様に、全ての p < 0 に対して
E
p
,
q
r
=
0
{\displaystyle E_{p,q}^{r}=0}
E
0
,
q
2
→
E
0
,
q
3
→
⋯
→
E
0
,
q
r
−
1
→
E
0
,
q
r
{\displaystyle E_{0,q}^{2}\to E_{0,q}^{3}\to \dots \to E_{0,q}^{r-1}\to E_{0,q}^{r}}
が存在する。これもエッジ写像と呼ばれている。
転入 (英語版 ) 部分対象から商への写像 (英語版 )
τ
:
E
p
,
0
2
→
E
0
,
p
−
1
2
{\displaystyle \tau :E_{p,0}^{2}\to E_{0,p-1}^{2}}
で、合成
E
p
,
0
2
→
E
p
,
0
p
→
d
E
0
,
p
−
1
p
→
E
0
,
p
−
1
2
{\displaystyle E_{p,0}^{2}\to E_{p,0}^{p}{\overset {d}{\to }}E_{0,p-1}^{p}\to E_{0,p-1}^{2}}
コホモロジー的なスペクトル系列
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
q < 0 に対して
E
r
p
,
q
=
0
{\displaystyle E_{r}^{p,q}=0}
E
2
p
,
0
→
E
3
p
,
0
→
⋯
→
E
r
−
1
p
,
0
→
E
r
p
,
0
{\displaystyle E_{2}^{p,0}\to E_{3}^{p,0}\to \dots \to E_{r-1}^{p,0}\to E_{r}^{p,0}}
が存在する。また、全ての p < 0 に対して
E
r
p
,
q
=
0
{\displaystyle E_{r}^{p,q}=0}
E
r
0
,
q
→
E
r
−
1
0
,
q
→
⋯
→
E
3
0
,
q
→
E
2
0
,
q
{\displaystyle E_{r}^{0,q}\to E_{r-1}^{0,q}\to \dots \to E_{3}^{0,q}\to E_{2}^{0,q}}
が存在する。
d
:
E
q
0
,
q
−
1
→
E
q
q
,
0
{\displaystyle d:E_{q}^{0,q-1}\to E_{q}^{q,0}}
τ
:
E
2
0
,
q
−
1
→
E
2
q
,
0
{\displaystyle \tau :E_{2}^{0,q-1}\to E_{2}^{q,0}}
は必ずしも well-defined な写像ではない。
これらの写像の決定を基礎として、セール・スペクトル系列 (英語版 )
d
n
:
E
n
,
0
n
→
E
0
,
n
−
1
n
{\displaystyle d_{n}:E_{n,0}^{n}\to E_{0,n-1}^{n}}
をホモロジー的なスペクトル系列に対して決定し、これをファイブレーション
F
→
E
→
B
{\displaystyle F\to E\to B}
d
n
:
H
n
(
B
)
→
H
n
−
1
(
F
)
{\displaystyle d_{n}:H_{n}(B)\to H_{n-1}(F)}
が得られる。
コホモロジー群にはカップ積 により環の構造 が入り、コホモロジー環 となる。したがって、スペクトル系列を同様に環の構造つきで考えることは自然なことである。
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
E
r
{\displaystyle E_{r}}
次数付き微分代数 であって、(ii)
E
r
+
1
{\displaystyle E_{r+1}}
E
r
{\displaystyle E_{r}}
典型的な例は、係数群が環 R であるときのファイブレーション
F
→
E
→
B
{\displaystyle F\to E\to B}
セール・スペクトル系列 (英語版 )
E
2
{\displaystyle E_{2}}
E
∞
{\displaystyle E_{\infty }}
E ; R ) と同型にはならない。乗法構造はスペクトル系列における微分の計算に非常に役に立つ。
スペクトル系列は様々な方法で作ることができる。代数的位相幾何学では、おそらく完全対による方法が最も一般的なものである。代数幾何学では、スペクトル系列は双対鎖複体のフィルトレーションから作られることが多い。
スペクトル系列を作るための最も強力な方法は、ウィリアム・マッセイ (英語版 ) [要出典 。にもかかわらず、(完全対は)抽象代数学ではあまり人気がなく、その分野ではほとんどのスペクトル系列はフィルターつき複体から得られている。完全対を定義するために、アーベル圏を1つとる。先程と同じく、応用上は大抵の場合環上の2重次数つき加群の圏である。完全対 とは、対象 A と C の対と、この対象間の3つの準同型: f : A → A , g : A → C and h : C → A であって、次の完全性の条件を満たすものを言う:
Image f = Kernel g Image g = Kernel h
Image h = Kernel f このデータを単に (A , C , f , g , h ) と表す。完全対は三角形の絵で表現することが多い。A を補助的なデータとして使い、E 0 項が C であるようなスペクトル系列を作ろう。
スペクトル系列の次のシートに行くために、導来対 (derived couple)をまず作る。次の記号を準備する:
d = g o h A' = f (A )C' = Ker d / Im d f' = f |A' f の A' への制限h' : C' → A' 、h から誘導されるもの。h がこのような写像を誘導することは簡単に分かる。g' : A' → C' は次のように定義する。A' の元 a に対して、A の元 b が存在して a は f (b ) と書ける。g' (a ) を、C' における g (b ) の像として定義する。一般の状況では、g' はアーベル圏に対する埋込み定理の一つを使って作られる。定義からすぐに (A' , C' , f' , g' , h' ) が完全対となることが分かる。C' をスペクトル系列の E1 項とする。この操作を繰り返して完全対の列 (A (n ) , C (n ) , f (n ) , g (n ) , h (n ) ) が得られ、C (n ) を En 項とし、dn を g (n ) o h (n ) と置くことで、求めるスペクトル系列になる。
スペクトル系列の極めて典型的な例はフィルターつきの (英語版 ) C• であって、全ての整数 p に対して部分複体 Fp C• が定義されており、境界写像はフィルトレーションと両立している、つまり d (Fp Cn ) ⊆ Fp C n +1p は上か下かどちらか片方で有界であることが多い。)フィルトレーションは減少 している、つまり Fp C• ⊇ F p +1C • と仮定する。双対鎖複体の項に対応する数字は n で表すことにする。あとではさらに、フィルトレーションはハウスドルフ (分離的 とも言う)、つまり Fp C• の全ての共通部分をとるとゼロであり、フィルトレーションは覆い尽くしている(exhaustive) 、つまり Fp C• の全ての和集合をとると鎖複体 C • 全体となることを仮定する。
フィルトレーションは0への近さを測るものとして便利である。p が大きくなるにつれて、Fp C• はゼロに近づいていく。このフィルトレーションから、あとのシートに行けば行くほどコバウンダリとコサイクルが元の複体のコバウンダリとコサイクルに近づいていくスペクトル系列が作れる。このスペクトル系列は、フィルター次数 p と補充次数 (complementary degree)q = n − p n よりも便利な添字であることが多い。例えば、あとで説明する2重複体のスペクトル系列の場合にそうである。)
このスペクトル系列を手作業で作ってみよう。C • は単一の次数づけとフィルトレーションしか持たないので、まず2重次数つき対象を C • から作る。第2の次数を得るために、フィルトレーションに随伴する次数つき対象を次のようにとる。
Z
−
1
p
,
q
=
Z
0
p
,
q
=
F
p
C
p
+
q
{\displaystyle Z_{-1}^{p,q}=Z_{0}^{p,q}=F^{p}C^{p+q}}
B
0
p
,
q
=
0
{\displaystyle B_{0}^{p,q}=0}
E
0
p
,
q
=
Z
0
p
,
q
B
0
p
,
q
+
Z
−
1
p
+
1
,
q
−
1
=
F
p
C
p
+
q
F
p
+
1
C
p
+
q
{\displaystyle E_{0}^{p,q}={\frac {Z_{0}^{p,q}}{B_{0}^{p,q}+Z_{-1}^{p+1,q-1}}}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}}}
E
0
=
⨁
p
,
q
∈
Z
E
0
p
,
q
{\displaystyle E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q}}
やや奇妙な書き方をしたが、こう書いた理由はあとで E 1 を作るときに分かる。境界写像はフィルトレーションと両立すると仮定しているので、E 0 は2重次数つき対象になっており、E 0 上に自然な2重次数つき境界写像 d 0 が存在する。E 1 を得るために E 0 のホモロジーをとる。
Z
¯
1
p
,
q
=
ker
d
0
p
,
q
:
E
0
p
,
q
→
E
0
p
,
q
+
1
=
ker
d
0
p
,
q
:
F
p
C
p
+
q
/
F
p
+
1
C
p
+
q
→
F
p
C
p
+
q
+
1
/
F
p
+
1
C
p
+
q
+
1
{\displaystyle {\bar {Z}}_{1}^{p,q}=\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}=\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}}
B
¯
1
p
,
q
=
im
d
0
p
,
q
−
1
:
E
0
p
,
q
−
1
→
E
0
p
,
q
=
im
d
0
p
,
q
−
1
:
F
p
C
p
+
q
−
1
/
F
p
+
1
C
p
+
q
−
1
→
F
p
C
p
+
q
/
F
p
+
1
C
p
+
q
{\displaystyle {\bar {B}}_{1}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}}
E
1
p
,
q
=
Z
¯
1
p
,
q
B
¯
1
p
,
q
=
ker
d
0
p
,
q
:
E
0
p
,
q
→
E
0
p
,
q
+
1
im
d
0
p
,
q
−
1
:
E
0
p
,
q
−
1
→
E
0
p
,
q
{\displaystyle E_{1}^{p,q}={\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}}
E
1
=
⨁
p
,
q
∈
Z
E
1
p
,
q
=
⨁
p
,
q
∈
Z
Z
¯
1
p
,
q
B
¯
1
p
,
q
{\displaystyle E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}=\bigoplus _{p,q\in \mathbf {Z} }{\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}}
Z
¯
1
p
,
q
{\displaystyle {\bar {Z}}_{1}^{p,q}}
B
¯
1
p
,
q
{\displaystyle {\bar {B}}_{1}^{p,q}}
Z
1
p
,
q
=
ker
d
0
p
,
q
:
F
p
C
p
+
q
→
C
p
+
q
+
1
/
F
p
+
1
C
p
+
q
+
1
{\displaystyle Z_{1}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+1}C^{p+q+1}}
B
1
p
,
q
=
(
im
d
0
p
,
q
−
1
:
F
p
C
p
+
q
−
1
→
C
p
+
q
)
∩
F
p
C
p
+
q
{\displaystyle B_{1}^{p,q}=({\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}
の
E
0
p
,
q
{\displaystyle E_{0}^{p,q}}
E
1
p
,
q
=
Z
1
p
,
q
B
1
p
,
q
+
Z
0
p
+
1
,
q
−
1
{\displaystyle E_{1}^{p,q}={\frac {Z_{1}^{p,q}}{B_{1}^{p,q}+Z_{0}^{p+1,q-1}}}}
となる。
Z
1
p
,
q
{\displaystyle Z_{1}^{p,q}}
B
1
p
,
q
{\displaystyle B_{1}^{p,q}}
Z
r
p
,
q
{\displaystyle Z_{r}^{p,q}}
r 上がるような要素全体、
B
r
p
,
q
{\displaystyle B_{r}^{p,q}}
r-1 だけ上がるような要素全体の像となることが推測できる。言い換えると、作ろうとしているスペクトル系列の項は
Z
r
p
,
q
=
ker
d
0
p
,
q
:
F
p
C
p
+
q
→
C
p
+
q
+
1
/
F
p
+
r
C
p
+
q
+
1
{\displaystyle Z_{r}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1}}
B
r
p
,
q
=
(
im
d
0
p
−
r
+
1
,
q
+
r
−
2
:
F
p
−
r
+
1
C
p
+
q
−
1
→
C
p
+
q
)
∩
F
p
C
p
+
q
{\displaystyle B_{r}^{p,q}=({\mbox{im }}d_{0}^{p-r+1,q+r-2}:F^{p-r+1}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}
E
r
p
,
q
=
Z
r
p
,
q
B
r
p
,
q
+
Z
r
−
1
p
+
1
,
q
−
1
{\displaystyle E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{B_{r}^{p,q}+Z_{r-1}^{p+1,q-1}}}}
と書けるはずで、さらに関係式
B
r
p
,
q
=
d
0
p
,
q
(
Z
r
−
1
p
−
r
+
1
,
q
+
r
−
2
)
{\displaystyle B_{r}^{p,q}=d_{0}^{p,q}(Z_{r-1}^{p-r+1,q+r-2})}
を満たすはずである。このようになるためには、各 Er 上の微分 dr であって、それによるホモロジーが上記の E r +1
d
r
p
,
q
:
E
r
p
,
q
→
E
r
p
+
r
,
q
−
r
+
1
{\displaystyle d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}}
は、
C
p
+
q
{\displaystyle C^{p+q}}
d を部分対象
Z
r
p
,
q
{\displaystyle Z_{r}^{p,q}}
この微分が先程の性質を持つこと、すなわち Er のこの微分によるホモロジーが E r +1
[ 編集 ] もう一つの典型的なスペクトル系列は2重複体のスペクトル系列である。2重複体 (double complex)とは、全ての整数 i と j を添え字に持つ対象 Ci,j の集まりと、2つの微分 d I と d II の組を合わせたものである。d I は i を減少させ、d II は j を減少させるものとする。さらに、 微分は反可換 (anticommute)、つまり d I d II + d II d I = 0 とする。目標は、2つのホモロジーのホモロジー、
H
i
I
(
H
j
I
I
(
C
∙
,
∙
)
)
{\displaystyle H_{i}^{I}(H_{j}^{II}(C_{\bullet ,\bullet }))}
H
j
I
I
(
H
i
I
(
C
∙
,
∙
)
)
{\displaystyle H_{j}^{II}(H_{i}^{I}(C_{\bullet ,\bullet }))}
(
C
i
,
j
I
)
p
=
{
0
if
i
<
p
C
i
,
j
if
i
≥
p
{\displaystyle (C_{i,j}^{I})_{p}={\begin{cases}0&{\text{if }}i<p\\C_{i,j}&{\text{if }}i\geq p\end{cases}}}
(
C
i
,
j
I
I
)
p
=
{
0
if
j
<
p
C
i
,
j
if
j
≥
p
{\displaystyle (C_{i,j}^{II})_{p}={\begin{cases}0&{\text{if }}j<p\\C_{i,j}&{\text{if }}j\geq p\end{cases}}}
これを前節の例にあてはめスペクトル系列を作ってみよう。まず、全複体 (total complex)T (C •,• ) を、n 次の項が
⨁
i
+
j
=
n
C
i
,
j
{\displaystyle \bigoplus _{i+j=n}C_{i,j}}
d I + d II で定義された複体とする。d I と d II は反可換な微分であることから、これは複体になっている。Ci,j の2つのフィルトレーションから、この全複体の2つのフィルトレーション
T
n
(
C
∙
,
∙
)
p
I
=
⨁
i
+
j
=
n
i
>
p
−
1
C
i
,
j
{\displaystyle T_{n}(C_{\bullet ,\bullet })_{p}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}}
T
n
(
C
∙
,
∙
)
p
I
I
=
⨁
i
+
j
=
n
j
>
p
−
1
C
i
,
j
{\displaystyle T_{n}(C_{\bullet ,\bullet })_{p}^{II}=\bigoplus _{i+j=n \atop j>p-1}C_{i,j}}
が得られる。このフィルトレーションのスペクトル系列からホモロジーのホモロジーについての情報が得られることを示すために、T (C •,• ) のフィルトレーション I についてのスペクトル系列の E 0 、E 1 、E 2 項を調べる。E 0 項は簡単で、
I
E
p
,
q
0
=
T
n
(
C
∙
,
∙
)
p
I
/
T
n
(
C
∙
,
∙
)
p
+
1
I
=
⨁
i
+
j
=
n
i
>
p
−
1
C
i
,
j
/
⨁
i
+
j
=
n
i
>
p
C
i
,
j
=
C
p
,
q
{\displaystyle {}^{I}E_{p,q}^{0}=T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}{\Big /}\bigoplus _{i+j=n \atop i>p}C_{i,j}=C_{p,q}}
となっている。ここで、n = p + q
E 1 項を明らかにするためには、E 0 での d I + d II を決定する必要がある。微分の次数は n に関して −1 であるから、次の写像
d
p
,
q
I
+
d
p
,
q
I
I
:
T
n
(
C
∙
,
∙
)
p
I
/
T
n
(
C
∙
,
∙
)
p
+
1
I
=
C
p
,
q
→
T
n
−
1
(
C
∙
,
∙
)
p
I
/
T
n
−
1
(
C
∙
,
∙
)
p
+
1
I
=
C
p
,
q
−
1
{\displaystyle d_{p,q}^{I}+d_{p,q}^{II}:T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q}\rightarrow T_{n-1}(C_{\bullet ,\bullet })_{p}^{I}/T_{n-1}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q-1}}
がある。
これから、E0 の微分は d I + d II から誘導される写像 C p ,q C p ,q −1d I の次数は異なっているので、d I は E 0 上でゼロでなければならない。これは、微分が d II と一致していることを意味しているので、
I
E
p
,
q
1
=
H
q
I
I
(
C
p
,
∙
)
{\displaystyle {}^{I}E_{p,q}^{1}=H_{q}^{II}(C_{p,\bullet })}
となる。E2 を明らかにするためには、
d
p
,
q
I
+
d
p
,
q
I
I
:
H
q
I
I
(
C
p
,
∙
)
→
H
q
I
I
(
C
p
+
1
,
∙
)
{\displaystyle d_{p,q}^{I}+d_{p,q}^{II}:H_{q}^{II}(C_{p,\bullet })\rightarrow H_{q}^{II}(C_{p+1,\bullet })}
を決定する必要がある。E 1 はちょうど d II についてのホモロジーだったので、d II は E 1 上でゼロになっている。したがって、
I
E
p
,
q
2
=
H
p
I
(
H
q
I
I
(
C
∙
,
∙
)
)
{\displaystyle {}^{I}E_{p,q}^{2}=H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))}
である。もう一方のフィルトレーションを使うと、同様の E 2 項を持つ異なるスペクトル系列
I
I
E
p
,
q
2
=
H
q
I
I
(
H
p
I
(
C
∙
,
∙
)
)
.
{\displaystyle {}^{II}E_{p,q}^{2}=H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet })).}
が得られる。あとはこの2つのスペクトル系列の関係がわかればよい。r が大きくなると、この2つのスペクトル系列は有用な比較ができるほど十分に似てくることがわかる。
一番はじめに議論した最も簡単な例(鎖複体のスペクトル系列 )では、1以上の r に対してスペクトル系列は停止した。このような状況ではシートの列の極限というものを合理的に考えることができる。0番目のシートの後には何も起こらないので、極限のシート E ∞ とは E 1 と思えば良い。
一般的な状況でも、シートの極限が存在することが多く、そして常に興味深いものになっている。この点が、スペクトル系列が強力な計算手法である理由の1つである。スペクトル系列
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
E
∞
p
,
q
{\displaystyle E_{\infty }^{p,q}}
収束する 、あるいは近づいていく(abuts to) [訳語疑問点 とは、ある r (p , q ) が存在して、全ての r ≥ r (p , q ) に対し微分
d
r
p
−
r
,
q
+
r
−
1
{\displaystyle d_{r}^{p-r,q+r-1}}
d
r
p
,
q
{\displaystyle d_{r}^{p,q}}
r に対して必然的に
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
E
∞
p
,
q
{\displaystyle E_{\infty }^{p,q}}
E
r
p
,
q
⇒
p
E
∞
p
,
q
{\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}}
という記号で表す。この p はフィルトレーションの添字を表現している。この表記法を使うとき、矢印の左側には、ほとんどのスペクトル系列で最も意味のある項
E
2
p
,
q
{\displaystyle E_{2}^{p,q}}
収束先(abutment) [訳語疑問点 と呼ばれる。
ほとんどのスペクトル系列において、
E
∞
{\displaystyle E_{\infty }}
E
∞
n
{\displaystyle E_{\infty }^{n}}
F
∙
E
∞
n
{\displaystyle F^{\bullet }E_{\infty }^{n}}
E
∞
p
,
q
=
gr
p
E
∞
p
+
q
=
F
p
E
∞
p
+
q
/
F
p
+
1
E
∞
p
+
q
{\displaystyle E_{\infty }^{p,q}={\mbox{gr}}_{p}E_{\infty }^{p+q}=F^{p}E_{\infty }^{p+q}/F^{p+1}E_{\infty }^{p+q}}
E
r
p
,
q
⇒
p
E
∞
n
{\displaystyle E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{n}}
と表記し、これで p + q = n の場合には
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
E
∞
p
,
q
{\displaystyle E_{\infty }^{p,q}}
収束を決定できる最も簡単な状況は、スペクトル系列が退化するときである。スペクトル系列がシート r で退化 するとは、任意の s ≥ r に対して微分 ds が零写像であることを言う。これは Er ≅ E r +1E r +2Er は E∞ と同型になる。これは、最初にあげたフィルター無しの鎖複体の自明な例(鎖複体のスペクトル系列 )で起きてたことである。あのスペクトル系列は1番目のシートで退化した。一般に、2重次数つきのスペクトル系列は、水平もしくは垂直な帯状領城の外でゼロならば退化する。先の方のシートでは、微分はその帯状領域の外の対象に対しての射か、もしくは外の対象からの射になるからである。
また、ある p 0 未満の全ての p と、ある q 0 未満の全ての q に対して
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
p 0 と q 0 を0で取ることができるとき、第1象限スペクトル系列 (first-quadrant spectral sequence)と呼ばれる。対象の、ゼロでない領域の境界からの距離は一定であることから、このようなスペクトル系列が収束することが分かる。結果的に、p と q を固定すると、後の方のシートでは微分は常に
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
p 0 より大きい全ての p と、ある q 0 より大きい全ての q に対して
E
r
p
,
q
{\displaystyle E_{r}^{p,q}}
スペクトル系列の5項完全系列 (英語版 ) E ∞ の項を関係付ける。
次の文献も参照のこと:
ボードマン、Conditionally Convergent Spectral Sequences
[ 編集 ] 包含関係の鎖(chain)
Z
0
p
,
q
⊇
Z
1
p
,
q
⊇
Z
2
p
,
q
⊇
⋯
⊇
B
2
p
,
q
⊇
B
1
p
,
q
⊇
B
0
p
,
q
{\displaystyle Z_{0}^{p,q}\supseteq Z_{1}^{p,q}\supseteq Z_{2}^{p,q}\supseteq \cdots \supseteq B_{2}^{p,q}\supseteq B_{1}^{p,q}\supseteq B_{0}^{p,q}}
を考える。下記のように置くと、何が起きるか考える。
Z
∞
p
,
q
=
⋂
r
=
0
∞
Z
r
p
,
q
{\displaystyle Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q}}
B
∞
p
,
q
=
⋃
r
=
0
∞
B
r
p
,
q
{\displaystyle B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q}}
E
∞
p
,
q
=
Z
∞
p
,
q
B
∞
p
,
q
+
Z
∞
p
+
1
,
q
−
1
{\displaystyle E_{\infty }^{p,q}={\frac {Z_{\infty }^{p,q}}{B_{\infty }^{p,q}+Z_{\infty }^{p+1,q-1}}}}
E
∞
p
,
q
{\displaystyle E_{\infty }^{p,q}}
r 個の非自明なステップからなる場合には、スペクトル系列は r 番目のシートの後で退化する。また、複体とフィルトレーションがともに下、もしくは上に有界ならば、収束する。
考えているスペクトル系列の収束先(abutment)をより詳細に記述するために、次の表示
Z
∞
p
,
q
=
⋂
r
=
0
∞
Z
r
p
,
q
=
⋂
r
=
0
∞
ker
(
F
p
C
p
+
q
→
C
p
+
q
+
1
/
F
p
+
r
C
p
+
q
+
1
)
{\displaystyle Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q}=\bigcap _{r=0}^{\infty }\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1})}
B
∞
p
,
q
=
⋃
r
=
0
∞
B
r
p
,
q
=
⋃
r
=
0
∞
(
im
d
p
,
q
−
r
:
F
p
−
r
C
p
+
q
−
1
→
C
p
+
q
)
∩
F
p
C
p
+
q
{\displaystyle B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q}=\bigcup _{r=0}^{\infty }({\mbox{im }}d^{p,q-r}:F^{p-r}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}
を考える。この表示から
Z
∞
p
,
q
{\displaystyle Z_{\infty }^{p,q}}
r が大きくなると、(最初の式に出てくる)核は縮小していき
Z
∞
p
,
q
=
ker
(
F
p
C
p
+
q
→
C
p
+
q
+
1
)
{\displaystyle Z_{\infty }^{p,q}=\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1})}
B
∞
p
,
q
{\displaystyle B_{\infty }^{p,q}}
r が大きくなると、(2番目の式に出てくる)像は大きくなっていき
B
∞
p
,
q
=
im
(
C
p
+
q
−
1
→
C
p
+
q
)
∩
F
p
C
p
+
q
{\displaystyle B_{\infty }^{p,q}={\text{im }}(C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}}
E
∞
p
,
q
=
gr
p
H
p
+
q
(
C
∙
)
{\displaystyle E_{\infty }^{p,q}={\mbox{gr}}_{p}H^{p+q}(C^{\bullet })}
が分かり、これからスペクトル系列の収束先(abutment)は C の (p+q) 番目のホモロジーの次数が p の部分になっていることが分かる。このスペクトル系列が収束するなら、
E
r
p
,
q
⇒
p
H
p
+
q
(
C
∙
)
{\displaystyle E_{r}^{p,q}\Rightarrow _{p}H^{p+q}(C^{\bullet })}
となることがわかった。
フィルターつき複体のスペクトル系列を使って、長完全系列 の存在を導くことができる。双対鎖複体の短完全系列 0 → A• → B• → C• → 0 を一つとり、最初の写像を f• : A• → B• とする。この系列のホモロジーを取って、自然な写像 Hn (A• ) → Hn (B• ) → Hn (C• ) が得られ、これは真ん中の部分で完全であることは知っている。フィルターつき複体のスペクトル系列を使ってこれの連結準同型を見つけ、そうやってできる列が完全であることを証明しよう。まず、B• のフィルターを
F
0
B
n
=
B
n
{\displaystyle F^{0}B^{n}=B^{n}}
F
1
B
n
=
A
n
{\displaystyle F^{1}B^{n}=A^{n}}
F
2
B
n
=
0
{\displaystyle F^{2}B^{n}=0}
で定義する。定義から、
E
0
p
,
q
=
F
p
B
p
+
q
F
p
+
1
B
p
+
q
=
{
0
if
p
<
0
or
p
>
1
C
q
if
p
=
0
A
q
+
1
if
p
=
1
{\displaystyle E_{0}^{p,q}={\frac {F^{p}B^{p+q}}{F^{p+1}B^{p+q}}}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\C^{q}&{\text{if }}p=0\\A^{q+1}&{\text{if }}p=1\end{cases}}}
E
1
p
,
q
=
{
0
if
p
<
0
or
p
>
1
H
q
(
C
∙
)
if
p
=
0
H
q
+
1
(
A
∙
)
if
p
=
1
{\displaystyle E_{1}^{p,q}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(C^{\bullet })&{\text{if }}p=0\\H^{q+1}(A^{\bullet })&{\text{if }}p=1\end{cases}}}
となる。微分は2重次数 (1, 0) を持つので、d0,q : Hq (C• ) → H q +1A• ) である。この写像は蛇の補題 による連結準同型で、写像 A• → B• → C• とあわせて列
⋯
→
H
q
(
B
∙
)
→
H
q
(
C
∙
)
→
H
q
+
1
(
A
∙
)
→
H
q
+
1
(
B
∙
)
→
⋯
{\displaystyle \cdots \rightarrow H^{q}(B^{\bullet })\rightarrow H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\rightarrow \cdots }
を得る。あとはこの列が A と C のところで完全であることを示せばよい。さきのスペクトル系列は、微分の2重次数は (2, −1) であるから、E 2 項で退化することに注意する。したがって、E 2 項は E ∞ 項と一致するので、
E
2
p
,
q
≅
gr
p
H
p
+
q
(
B
∙
)
=
{
0
if
p
<
0
or
p
>
1
H
q
(
B
∙
)
/
H
q
(
A
∙
)
if
p
=
0
im
H
q
+
1
f
∙
:
H
q
+
1
(
A
∙
)
→
H
q
+
1
(
B
∙
)
if
p
=
1
{\displaystyle E_{2}^{p,q}\cong {\text{gr}}_{p}H^{p+q}(B^{\bullet })={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(B^{\bullet })/H^{q}(A^{\bullet })&{\text{if }}p=0\\{\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })&{\text{if }}p=1\end{cases}}}
が成り立つ。E 2 項は、これに加えて E 1 項のホモロジーとしての直接的な記述を持つ。この2つの記述の記述を比べて、同型
H
q
(
B
∙
)
/
H
q
(
A
∙
)
≅
ker
d
0
,
q
1
:
H
q
(
C
∙
)
→
H
q
+
1
(
A
∙
)
{\displaystyle H^{q}(B^{\bullet })/H^{q}(A^{\bullet })\cong \ker d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })}
im
H
q
+
1
f
∙
:
H
q
+
1
(
A
∙
)
→
H
q
+
1
(
B
∙
)
≅
H
q
+
1
(
A
∙
)
/
(
im
d
0
,
q
1
:
H
q
(
C
∙
)
→
H
q
+
1
(
A
∙
)
)
{\displaystyle {\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\cong H^{q+1}(A^{\bullet })/({\mbox{im }}d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet }))}
を得る。1番目の式から C のところでの完全性が従い、2番目の式から A のところでの完全性が従う。
フィルターつき複体についての収束先(abutment)を使うと、
H
p
I
(
H
q
I
I
(
C
∙
,
∙
)
)
⇒
p
H
p
+
q
(
T
(
C
∙
,
∙
)
)
{\displaystyle H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))\Rightarrow _{p}H^{p+q}(T(C_{\bullet ,\bullet }))}
H
q
I
I
(
H
p
I
(
C
∙
,
∙
)
)
⇒
q
H
p
+
q
(
T
(
C
∙
,
∙
)
)
{\displaystyle H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet }))\Rightarrow _{q}H^{p+q}(T(C_{\bullet ,\bullet }))}
が分かる。一般には、Hp+q (T(C•,• )) 上の2つの次数付けは異なる 。にもかかわらず、この2つのスペクトル系列から有益な情報を得ることが可能である。
R を環、M を右 R 加群、N を左 R 加群とする。テンソル積の導来関手を Tor と表していたことを思い出そう。これは最初の引数の射影分解 を使って定義されていたが、実は
Tor
i
(
M
,
N
)
=
Tor
i
(
N
,
M
)
{\displaystyle \operatorname {Tor} _{i}(M,N)=\operatorname {Tor} _{i}(N,M)}
M と N の射影分解を一つとり、それぞれ
P
∙
{\displaystyle P_{\bullet }}
Q
∙
{\displaystyle Q_{\bullet }}
d と e とする。2重複体を、項は
C
i
,
j
=
P
i
⊗
Q
j
{\displaystyle C_{i,j}=P_{i}\otimes Q_{j}}
d
⊗
1
{\displaystyle d\otimes 1}
(
−
1
)
i
(
1
⊗
e
)
{\displaystyle (-1)^{i}(1\otimes e)}
射影加群は平坦 なので、射影加群をテンソルする操作とホモロジーを取る操作は交換可能である。したがって、
H
p
I
(
H
q
I
I
(
P
∙
⊗
Q
∙
)
)
=
H
p
I
(
P
∙
⊗
H
q
I
I
(
Q
∙
)
)
{\displaystyle H_{p}^{I}(H_{q}^{II}(P_{\bullet }\otimes Q_{\bullet }))=H_{p}^{I}(P_{\bullet }\otimes H_{q}^{II}(Q_{\bullet }))}
H
q
I
I
(
H
p
I
(
P
∙
⊗
Q
∙
)
)
=
H
q
I
I
(
H
p
I
(
P
∙
)
⊗
Q
∙
)
{\displaystyle H_{q}^{II}(H_{p}^{I}(P_{\bullet }\otimes Q_{\bullet }))=H_{q}^{II}(H_{p}^{I}(P_{\bullet })\otimes Q_{\bullet })}
が成り立つ。2つの複体は分解になっているので、そのホモロジーは次数0部分を除き消える。次数0部分には
H
p
I
(
P
∙
⊗
N
)
=
Tor
p
(
M
,
N
)
{\displaystyle H_{p}^{I}(P_{\bullet }\otimes N)=\operatorname {Tor} _{p}(M,N)}
H
q
I
I
(
M
⊗
Q
∙
)
=
Tor
q
(
N
,
M
)
{\displaystyle H_{q}^{II}(M\otimes Q_{\bullet })=\operatorname {Tor} _{q}(N,M)}
が残っている。特に、
E
p
,
q
2
{\displaystyle E_{p,q}^{2}}
I スペクトル系列については q = 0 の直線部分を除き消え、II スペクトル系列については p = 0 の直線部分を除き消える。これから2番目シートでスペクトル系列は退化していることが分かり、したがって E ∞ 項は E 2 項と同型である:
Tor
p
(
M
,
N
)
≅
E
p
∞
=
H
p
(
T
(
C
∙
,
∙
)
)
{\displaystyle \operatorname {Tor} _{p}(M,N)\cong E_{p}^{\infty }=H_{p}(T(C_{\bullet ,\bullet }))}
Tor
q
(
N
,
M
)
≅
E
q
∞
=
H
q
(
T
(
C
∙
,
∙
)
)
{\displaystyle \operatorname {Tor} _{q}(N,M)\cong E_{q}^{\infty }=H_{q}(T(C_{\bullet ,\bullet }))}
p と q が等しければ両式の右辺は等しいので、これで Tor の可換性が示せた。
有名なスペクトル系列を以下に列挙する。
^ Jean Leray (1946a , 1946b )^ #Hilton p.256.^ #Stacks p.55.^ #Hilton p.257.^ #河田 pp.183-184.^ a b c #Stacks p.52.
^ #Rotman p.624.^ #玉木-完全対とスペクトル系列の基本 ^ #EoM ^ #McCleary p.455.^ #Hilton p.261.^ #Stacks p.55.^ #Hilton pp.257-258.^ #安藤 p.143.^ #Hatcher p.522^ #Rotman p.620^ #Hilton p.258.^ #安藤 p.143.^ #安藤 p.143.^ #MacLane p.337.^ #Rotman p.622.^ a b #Hilton pp.257-258.
^ #Hilton p.258.^ #Stacks p.46.^ #Stacks p.46.^ #Hilton p.261.^ #Hilton p.261.^ #Hilton p.262.^ #Stacks p.60.^ #安藤 p.146.^ #Stacks p.61.^ #Rotman p.619.^ a b #Hilton pp.263-264.
^ a b #Rotman pp.621-622.
^ Weibel 1994 , Exercise 5.2.1.; there are typos in the exact sequence, at least in the 1994 edition.^ Weibel 1994 , Exercise 5.2.2.^ Weibel 1994 , Application 5.3.5.^ Elzein, Fouad; Trang, Lê Dung (23 February 2013). "Mixed Hodge Structures". pp. 40, 4.0.2. arXiv :1302.5811 math.AG ]。 ^ Bruner, Robert R.; Rognes, John (2005). “Differentials in the homological homotopy fixed point spectral sequence”. Algebr. Geom. Topol. 5 (2): 653-690. arXiv :math/0406081 . doi :10.2140/agt.2005.5.653 .
^ このファイバー積における
Z
r
+
1
↪
Z
r
{\displaystyle Z^{r+1}\hookrightarrow Z^{r}}
Z
r
+
1
↠
K
e
r
d
r
{\displaystyle Z^{r+1}\twoheadrightarrow \mathrm {Ker} d^{r}}
[5]
B
r
+
1
{\displaystyle B^{r+1}}
^ アーベル圏におけるチェイン複体のなす圏はアーベル圏になる事が知られているので、以下のものは上述のチェイン複体のものの一般化になっている。
^ a b
すなわちα2 は以下を可換にする写像である:
D
1
→
β
1
I
m
β
1
=
K
e
r
γ
1
⊂
K
e
r
β
1
∘
γ
1
=
K
e
r
d
1
↓
α
1
↺
↓
π
D
2
=
I
m
α
1
−
−
−
−
−
−
−
−
−
−
−
→
β
2
E
2
=
K
e
r
d
1
/
I
m
d
1
{\displaystyle {\begin{array}{ccccc}D^{1}&{\overset {\beta ^{1}}{\to }}&\mathrm {Im} \beta ^{1}=\mathrm {Ker} \gamma ^{1}&\subset &\mathrm {Ker} \beta ^{1}\circ \gamma ^{1}=\mathrm {Ker} d^{1}\\\downarrow \alpha ^{1}&&\circlearrowleft &&\downarrow \pi \\D^{2}=\mathrm {Im} \alpha ^{1}&&{\overset {\beta ^{2}}{-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!\to }}&&E^{2}=\mathrm {Ker} d^{1}/\mathrm {Im} d^{1}\end{array}}}
γ2 は以下を可換にする写像である:
K
e
r
d
1
⊂
E
1
→
γ
1
D
1
↓
π
↺
↓
α
1
E
2
=
K
e
r
d
1
/
I
m
d
1
−
−
−
−
−
−
−
−
→
γ
2
D
2
{\displaystyle {\begin{array}{rcl}\mathrm {Ker} d^{1}&\subset ~~E^{1}~~{\overset {\gamma ^{1}}{\to }}&D^{1}\\\downarrow \pi &\circlearrowleft &\downarrow \alpha ^{1}\\E^{2}=\mathrm {Ker} d^{1}/\mathrm {Im} d^{1}&{\overset {\gamma ^{2}}{-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-\!\!\!\to }}&D^{2}\end{array}}}
^ 添字の番号が1から始まる事から
(
D
1
,
E
1
,
α
1
,
β
1
,
γ
1
)
{\displaystyle (D^{1},E^{1},\alpha ^{1},\beta ^{1},\gamma ^{1})}
[19]
^ 本項では多くの文献[30] [31] [32] H の添字を「
H
p
+
q
{\displaystyle H_{p+q}}
H
q
{\displaystyle H_{q}}
[33]
Peter J. Hilton, Urs Stammbach (2012/9/5). A Course in Homological Algebra . Graduate Texts in Mathematics . 4 (second ed.). Springer New York. ISBN 978-1-4419-8566-8 Joseph J. Rotman (2008/12/10). An Introduction to Homological Algebra . Universitext (second ed.). Springer-Verlag (Originally published by Academic Press, 1979). ISBN 978-0-387-68324-9 Allen Hatcher. “Spectral Sequences in Algebraic Topology ”. Cornel University. 2021年9月24日 閲覧。 //下記の書籍のために書いたが、結局書籍に載せなかったものを著者自身がウェブ公開[1] Allen Hatcher (2001/11/15). Algebraic Topology . Cambridge University Press. ISBN 978-0521795401 河田敬義『ホモロジー代数』岩波書店 〈岩波基礎数学選書〉、1990年11月8日。ISBN 978-4000078047 。 安藤哲哉『ホモロジー代数学』数学書房 、2010年2月1日。ISBN 978-4903342160 。 R. ボット , L.W. トゥー 『微分形式と代数トポロジー』シュプリンガー・フェアラーク東京、1996年11月1日。ISBN 978-4431707073 。 John McCleary (2000/9/15). A User's Guide to Spectral Sequences . Cambridge Studies in Advanced Mathematics. 58 (second ed.). Cambridge University Press. ISBN 978-0521567596 Charles Weibel (2008/1/12). Introduction to Homological Algebra . Cambridge Studies in Advanced Mathematics. 38 (Revised ed.). Cambridge University Press. ISBN 978-0521559874 玉木大(信州大学教授). “Algebraic Topology: A guide to literature ”. 2023年12月27日 閲覧。
玉木大(信州大学教授). “スペクトル系列 ”. Algebraic Topology: A guide to literature . 2023年12月27日 閲覧。 玉木大(信州大学教授). “完全対とスペクトル系列の基本 ”. Algebraic Topology: A guide to literature . 2023年12月27日 閲覧。 Aise Johan de Jong. “The Stacks project ”. Columbia University . 2023年12月28日 閲覧。
Saunders Mac Lane (2012/12/06). Homology . Classics in Mathematics (Originally published as volume 114 in the series: Grundlehren der mathematischen). Springer Berlin, Heidelberg. ISBN 978-3-642-62029-4 May, J. Peter . “A primer on spectral sequences ”. 2020年6月21日時点のオリジナルよりアーカイブ 。2020年6月21日 閲覧。McCleary, John (2001). A User's Guide to Spectral Sequences . Cambridge Studies in Advanced Mathematics. 58 (2nd ed.). Cambridge University Press . doi :10.2277/0521567599 . ISBN 978-0-521-56759-6 . MR 1793722 Fomenko, Anatoly; Fuchs, Dmitry, Homotopical Topology , http://www.math.columbia.edu/~khovanov/algtop2013/ “Spectral sequence ”. Encyclopedia of Mathematics . 2024年1月18日 閲覧。 Leray, Jean (1946a), “L'anneau d'homologie d'une représentation”, Les Comptes rendus de l'Académie des sciences 222 : 1366–1368 Leray, Jean (1946b), “Structure de l'anneau d'homologie d'une représentation”, Les Comptes rendus de l'Académie des sciences 222 : 1419–1422 Koszul, Jean-Louis (1947). “Sur les opérateurs de dérivation dans un anneau”. Comptes rendus de l'Académie des Sciences 225 : 217–219. Massey, William S. (1952). “Exact couples in algebraic topology. I, II”. Annals of Mathematics 56 (2): 363–396. doi :10.2307/1969805 . JSTOR 1969805 . Massey, William S. (1953). “Exact couples in algebraic topology. III, IV, V”. Annals of Mathematics 57 (2): 248–286. doi :10.2307/1969858 . JSTOR 1969858 . Mosher, Robert; Tangora, Martin (1968), Cohomology Operations and Applications in Homotopy Theory , Harper and Row, ISBN 978-0-06-044627-7 Weibel, Charles A. (1994), An introduction to homological algebra , Cambridge Studies in Advanced Mathematics, 38 , Cambridge University Press , ISBN 978-0-521-55987-4 , OCLC 36131259 , MR 1269324
^ Allen Hatcher. “Chapter 5. Spectral Sequences ”. Cornel University. 2023年12月27日 閲覧。


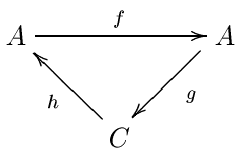




































































![{\displaystyle \beta ^{2}(\alpha ^{1}(x))=[\beta ^{1}(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44df03ee0fbc557f3295d3d42776683169eb3615)
![{\displaystyle \gamma ^{2}([z])=\gamma ^{1}(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8738ffa41ee6b4b82547189863f598597acf9125)
![{\displaystyle [\cdot ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41b4e841c71afe1890198191aab15bc225bbc0b6)






















































































































































































































































